Stokes’ Law - Terminal Velocity

A spherical ball of density $\text{ρ}$ and radius $0.003 \mathrm{m}$ is dropped into a tube containing a viscous fluid, filled up to the $0 \mathrm{cm}$ mark as shown in the figure. Viscosity of the fluid =$1.260 \mathrm{N} {\mathrm{m}}^{-2} {\mathrm{s}}^{-1}$ and its density ${\text{ρ}}_{\text{L}}$ = $\text{ρ}/2=1260 \mathrm{kg} {\mathrm{m}}^{-3}$. Assume the ball reaches a terminal speed by the $10 \mathrm{cm}$ mark. Find the time taken by the ball to traverse the distance between the $10 \mathrm{cm}$ and $20 \mathrm{cm}$ mark. [$\mathrm{g}$ = acceleration due to gravity = $10 \mathrm{m} {\mathrm{s}}^{-2}$^​​ ]

A spherical ball of radius $\text{1}\times 10^{-4} \mathrm{m}$ and density $104 \mathrm{kg} {\mathrm{m}}^{-3}$^​ falls freely under gravity through a distance $h$ before entering a tank of water. If after entering the water the velocity of the ball does not change, find $h$. The viscosity of water is $9.8\times 10^{-6} {\mathrm{Nsm}}^{-2}$.

The velocity of a small ball of mass $m$ and density $d_1$, when dropped in a container filled with glycerine, becomes constant after some time. If the density of glycerine is $d_2$, then the viscous force acting on the ball, will be

A water drop of radius $1\mu \mathrm{m}$ falls in a situation where the effect of buoyant force is negligible. Co-efficient of viscosity of air is $1.8\times {10}^{-5} \mathrm{N} \mathrm{s} {\mathrm{m}}^{-2}$ and its density is negligible as compared to that of water ${10}^6 \mathrm{g} {\mathrm{m}}^{-3}$. Terminal velocity of the water drop is

(Take acceleration due to gravity $=10{ \mathrm{m} \mathrm{s}}^{-2}$)

The terminal velocity $\left(v_t\right)$ of the spherical rain drop depends on the radius $\left(r\right)$ of the spherical rain drop as 

A raindrop falling in air is similar to motion of what kind of body in viscous medium?

Terminal speed of $2 \mathrm{cm}$ radius ball in a viscous liquid is $20 \mathrm{c}\mathrm{m }{\mathrm{s}}^{-1}$. Then the terminal speed of $1 \mathrm{cm}$ radius ball in the same liquid is

Which of the following option correctly describes the variation of the speed $\mathrm{\upsilon }$ and acceleration 'a' of a point mass falling vertically in a viscous medium that applies a force $\mathrm{F}=-\mathrm{k}\mathrm{\upsilon }$ , where 'k' is a constant, on the body? (Graphs are schematic and not drown to scale)

When a ball is released from rest in a very long column of viscous liquid, its downward acceleration is $a$ (just after release). Its acceleration, when it has acquired two-third of the maximum velocity, is

The terminal velocity $v$ of a spherical ball of lead of radius $R$ falling through a viscous liquid varies with $R$ such that

A raindrop of radius $0.3 \mathrm{mm}$ has a terminal velocity in air $=1 \mathrm{m }{\mathrm{s}}^{-1}$. The viscous force on it is (Given the viscosity of the air is $18 \times {10}^{-5} \mathrm{g} {\mathrm{cm}}^{-1} {\mathrm{s}}^{-1}$)

If a ball of steel $({\mathrm{\rho }}_{\mathrm{ball}}=7.8 \mathrm{g} {\mathrm{cm}}^{-3})$ attains a terminal velocity of $10 \mathrm{cm} {\mathrm{s}}^{-1}$ when falling in water $\left({\mathrm{\eta }}_{\mathrm{water}}=8.5 \times {10}^{-4} \mathrm{Pa} \mathrm{s}\right)$, then its terminal velocity in glycerine $\left({\mathrm{\sigma }}_{\mathrm{glycerine}}=1.2 \mathrm{g} {\mathrm{cm}}^{-3}, {\mathrm{\eta }}_{\mathrm{glycerine}}=13.2 \mathrm{Pa} \mathrm{s}\right)$ would nearly be,

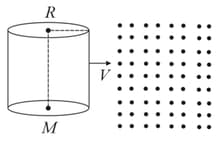
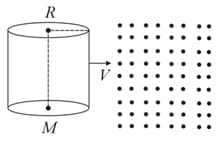
A cylinder of mass $M$ and radius $R$ moves with constant speed $v$ through a region of space that contains dust particles of mass $m$ which are at rest. There are $n$ number of particles per unit volume. The cylinder moves in a direction perpendicular to its axis. Assume $m<<M$ and that the particles do not interact with each other. All the collisions taking place are perfectly elastic and the surface of the cylinder is smooth. The drag force per unit length of the cylinder required to maintain a speed $v$ constant for the cylinder when it has entered a region is $\frac{K}{3}nmR{v}^2$. Find the value of $K$.

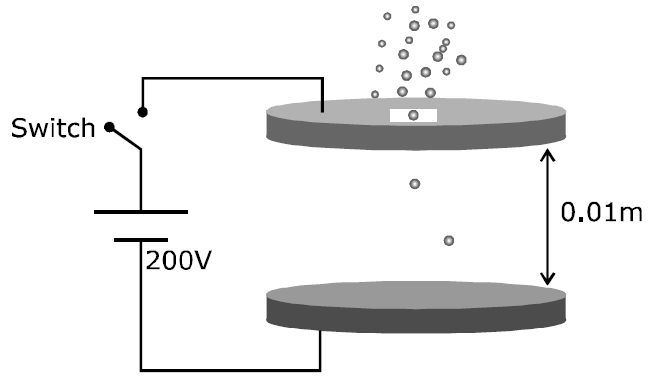
Two large circular discs separated by a distance of $0.01 \mathrm{m}$ are connected to a battery via a switch as shown in the figure. Charged oil drops of density $900 \mathrm{kg} {\mathrm{m}}^{-3}$ are released through a tiny hole at the centre of the top disc. Once some oil drops achieve terminal velocity, the switch is closed to apply a voltage of $200 \mathrm{V}$ across the discs. As a result, an oil drop of radius $8\times {10}^{-7} \mathrm{m}$ stops moving vertically and floats between the discs. The number of electrons present in this oil drop is (neglect the buoyancy force, take acceleration due to gravity $=10 {\mathrm{ms}}^{-2}$ and charge on an electron $\left.\left(e\right)=1.6\times {10}^{-19}\mathrm{C}, \mathrm{\pi }=3.14\right)$

A lead ball of $1 \mathrm{mm}$ diameter falls through a long column of glycerine. The variation of its velocity with distance covered is represented by

A raindrop reaching the ground with terminal velocity has momentum $p$. Another drop of twice the radius, also reaching the ground with terminal velocity, will have momentum

A small spherical ball of radius $r$ and density $\sigma$ is released from height $h$ above the liquid surface of density $\rho$ and viscosity $\eta .$The value of $h$ if the velocity of sphere inside the liquid remains constant is

A metallic sphere having density ${\rho }_s$ falls in glycerin of density ${\rho }_g,$ which is kept in a cylindrical container of radius $R$ and a very large height $h.$

Assume that the acceleration due to gravity is $g,$ that the radius of the sphere is a and that the viscosity of glycerin is very large $\left(\eta \right).$

(P) The terminal speed of the sphere is $v_T=\frac{2}{9}\left({\rho }_s-{\rho }_g\right)\frac{a^2 g}{\eta }.$

(Q) The terminal speed of the sphere $v_T<\frac{2}{9}\left({\rho }_s-{\rho }_g\right)\frac{a^2 g}{\eta }.$

(R) The viscous force acting on the sphere is $6\pi \eta av.$

(S) The viscous force acting on the sphere is greater than $6\mathrm{\pi }\eta av.$

Consider the statements ABOVE and select the correct option BELOW

The velocity of small ball of mass $m$ and density $\rho$ when dropped in a container filled with glycerine of density $\sigma$ becomes constant after sometime. The viscous force acting on the ball in the final state is : -

A metallic sphere having density ${\rho }_{\mathrm{s}}$ falls in glycerin of density ${\rho }_{\mathrm{g}}$, which is kept in a cylindrical container of radius $R$ and a very large height $h$. Assume that the acceleration due to gravity is $\mathrm{g}$, that the radius of the sphere is a and that the viscosity of glycerin is very large $\left(\eta \right)$.

(P) The terminal speed of the sphere is $v_T=\frac{2}{9} \left({\rho }_{\mathrm{s}}-{\rho }_{\mathrm{g}}\right) \frac{a^{2}g}{\eta }$.

(Q) The terminal speed of the sphere $v_T<\frac{2}{9} \left({\rho }_s-{\rho }_g\right) \frac{a^{2}g}{\eta }$.

(R) The viscous force acting on the sphere is $6\pi \eta av$.

(S) The viscous force acting on the sphere is greater than $6\pi \eta av$. Consider the statements ABOVE and select the correct option BELOW